고등학교 수학으로 탐구하는 생명과학의 다인자 유전
#1 다항식 계산, 확률과 통계의 조합, 정규분포와 다인자 유전
다인자 유전학이란
다인자 유전의 예시
여기에 사용되는 다양한 수학 기법들
다양한 질병들과 다인자 유전학
다인자 유전이란
정의 설명
멘델의 유전법칙을 배웠습니다.
우열의 원리(우열의 법칙에서 원리로 변경 why? 분홍색 꽃 때문)
분리의 법칙
독립의 법칙
다인자 유전(다원성 유전)은 하나의 특성이 여러 개의 유전자에 의해 결정되는 현상을 말합니다. 이는 단일 유전자의 영향만으로 설명되기 어려운 복잡한 현상들을 이해하는 데 도움이 됩니다.
실제 우리 주변에 발현되는 다양한 현상은 단순 요인으로 발생하지 않습니다.
예를 들어 보겠습니다.
피부색이 3가지 대립되는 유전형질로 다양한 표현형을 가집니다.
여기서 다인자 유전으로 연속되는 형태를 가진다고 합시다.
대립 형질 중 대문자가 어두운 피부색 소문자가 밝은 피부색이라고 합시다.
그리고 대문자가 우성이라고 하겠습니다.
물론 실제 피부색을 결정하는 유전인자는 3쌍 이상일 것입니다.
여기서는 설명을 위해 간략히 다룹니다.
일단 이해를 위해 나열하겠습니다.
Aa
Bb
Cc
1단계 매우 어두운 피부 AABBCC
2단계 어두운 피부 aABBCC, AaBBCC, AAbBCC, AABbCC, AABBcC, AABBCc
3단계 약간 어두운 피부 aaBBCC, aAbBCC, aABbCC, aABBcC, aABBCc, AabBCC, AaBbCC, AaBBcC, AaBBCc, AAbbCC, AAbBcC, AAbBCc, AABbcC, AABbCc, AABBcc
4단계 중간 피부 aabBCC, aaBbCC, aaBBcC, aaBBCc, aAbbCC, aAbBcC, aAbBCc, aABbcC, aABbCc, aABBcc, AabbCC, AabBcC, AabBCc, AaBbcC, AaBbCc, AaBBcc, AAbbcC, AAbbCc, AAbBcc, AABbcc
5단계 약간 밝은 피부 aabbCC, aabBcC, aabBCc, aaBbcC, aaBbCc, aaBBcc, aAbbcC, aAbbCc, aAbBcc, aABbcc, AabbcC, AabbCc, AabBcc, AaBbcc, AAbbcc
6단계 밝은 피부 aabbcC, aabbCc, aabBcc, aaBbcc, aAbbcc, Aabbcc
7단계 매우 밝은 피부 aabbcc
전체 유전 형질이 조합이 되는 전체 경우의 수는 64가지 이며, 이를 바탕으로 7가지 표현형이 나옵니다.
일단 전체가 64개가 되는 이유는 간단합니다.
우리는 6개의 유전자의 자리에 우성인자(대문자)와 열성인자(소문자)중 하나를 선택합니다.
즉, 2x2x2x2x2x2= 2^6 = 64입니다.
이제 여기에 다양한 수학적 기법을 사용해서 해당 내용을 분석해 보겠습니다.
먼저 고등학교 1학년 수준으로 다항식을 기반으로 해당 내용을 분석해 보겠습니다.
위의 내용은 사람이 결국 6개의 피부색 관련 유전 인자를 가지고 여섯 개의 유전 인자 중 몇 개가 우성(대문자)인지에 따라 피부색의 밝기가 결정되는 모양새입니다.
여기서 중요한건 어떤 유전인자인지는 중요하지 않습니다. 즉, 문자의 캐릭터 A, B, C는 중요하지 않다는 겁니다.
AABbcc나 AaBbCc나 모두 같은 피부색을 가진다는 것입니다.
이를 다항식으로 살펴 보겠습니다.
간단한 다항식 모델을 보겠습니다.

=(x+1)(x+1)(x+1)(x+1)(x+1)(x+1)(x+1)입니다.
이를 우리가 실제 나열하면서 그 결과를 구한다고 합시다.
그렇다면 우린 하나의 괄호 안에서 하나의 문자만 선택합니다.
결과 값을 살펴보면, 아래와 같습니다.

위 식에서 x에 관한 6차 항은 즉 x의 6제곱은 다항식의 곱셉의 각 괄호에서 x만 계속 선택해서 x만 여섯 번을 선택한 경우입니다.
마찬가지로 x에 관한 5차 항은 x를 다섯 번 선택하고 한번은 x가 아닌 1을 선택해서 곱했다는 뜻이죠.
첫 번째 괄호에서 1을 택하는 방법, 두 번째 괄호에서 1을 택하는 방법, .... ,마지마 번째 괄호에서 1을 택하는 방법까지 총 6가지가 존재합니다.
즉 x의 5제곱은 6개가 되고, 때문에 위 식의 x의 5차항의 계수는 6이 됩니다.
이제 위 다항식을 이렇게 바꿔 써 보겠습니다.
(A+a)(A+a)(B+b)(B+b)(C+c)(C+c)
하나의 항만 구해 보겠습니다.
첫 번째 괄호에서 A를 선택, 두 번째 괄호에서 a선택, 이후 B, B, C, c를 선택해서 곱했다고 하겠습니다.
그러면 그 결과는 AaBBCc가 나올 것입니다. 우리가 위에서 나열한 것 중에 하나가 나옵니다.
감이 좀 잡히시죠?
이제 합쳐 봅시다. 분명 문자의 종류는 상관없다고 했습니다.
그렇다면 위의 다항식을
(A+a)(A+a)(A+a)(A+a)(A+a)(A+a)로 표현해서 얻은 결과
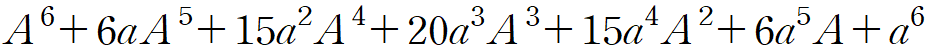
는 (A+a)(A+a)(B+b)(B+b)(C+c)(C+c)를 계산해서 얻은 결과와 같은 것을 말해준다는 것을 알 수 있습니다.
그리고 이는 사실
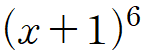
으로 나온
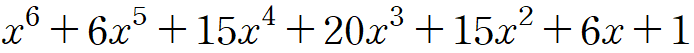
위 식과 같은 내용을 설명할 수 있습니다.
이미 눈치채셨겠지만, 우리가 각 표현형이 나오는 경우의 수와 다항식의 계수가 일치합니다.
또한 표현형의 종류가 항의 개수와 일치하게 됩니다.
만약 확률과 통계의 조합을 배웠다면 다항식의 계수를 조합을 통해 구할 수 있다는 것을 알고 있을 것이고
위 설명을 조합으로 이해 및 표현 할 수 있을 것입니다.
그리고 반대의 생각도 가능 할 것입니다. 특정한 표현형이 정규분포를 이루고 있다면 이를 다인자 유전으로 해석해 볼 수도 있으 ㄹ것비니다.
이를 통해서 특정 유전형의 연구를 다항식의 계산, 통계적 기법을 통해 예측해 볼 수 있으며,
만약 빅데이터를 통해 특정 표현형의 비, 분포를 알 수 있다면
해당 표현에 영향을 끼치는 유전자 쌍의 개수를 추측해 보는 것이 가능할 수도 있습니다.
다만,
다인자 유전은 유전적 변이와 환경 요인의 복합적인 영향을 통해 나타납니다. 예를 들어, 심혈관 질환, 당뇨병, 고혈압과 같은 복잡한 질환은 여러 유전자와 환경적 요인의 조합으로 발생하는 경우가 많습니다. 이러한 복잡한 질환은 하나의 유전자 변이만으로는 설명되기 어렵고, 다양한 유전자 간의 조합과 상호작용, 그리고 환경적인 요인들이 복합적으로 작용하여 발생하는 것이 특징입니다.
다 많은 요소를 복학접으로 생각하려면 더 좋은 모델을 구축해야 할 것이고 위의 방법은 그 기초를 제공 할 수 있을 것입니다.
'교육(학업) > 수학 탐구' 카테고리의 다른 글
| 최근 수학 교육 연구 동향 (0) | 2023.05.02 |
|---|---|
| 최근 수학 교육 연구 동향 (0) | 2023.04.26 |
| 생명과학, 사회학 심리학 현상의 수학적 해석(로그를 활용한 베버 페히너 법칙 탐구) (1) | 2022.09.12 |