선형회귀법의 수학적 원리(2) - 선형회귀식 찿는법(numpy.linalg.pinv)

[주요단어]

인공지능, 선형회귀, 파이썬, numpy, linalg pinv inv 행렬 수학 활용 벡터 직선의 방정식 연립 역행렬 가짜 유사 의사 무어-펜로즈 유사역행렬(Moore-Penrose) 컴퓨터 프로그래밍, AI, 경향성 예측

 

혹시 행렬을 모르시는 분은 1편 기초 행렬을 보시면 이해하시도록 행렬 기초 내용을 넣었습니다.

1편을 꼭 보고와 주세요

 

해당 내용은 가장 아래 유튜브 링크되어 있습니다. 읽는게 귀찮으신 분은

가장 아래쪽으로 내려가시면 유튜브 링크해 놓겠습니다.

 

2부 선형 회귀식(numpy.linalg.pinv는 어떻게 작동되는가?)

:실제 많은 사람들이 사용하지만 어떻게 작동되는지 수학적 원리를 확인해 보겠습니다.

① 역행렬로 방정식 풀기

아래와 같은 행렬 A가 있고, a,b의 값을 찾으려 한다고 합시다.

 

우리가 3x=9 의 해를 찾을 때, 양변에 1/3을 곱해 x의 값을 찾듯이

위 행렬로 이루어진 방정식도 양변의 왼쪽에 A의 역행를을 곱새 a, b의 값을 찾을 수 있습니다.

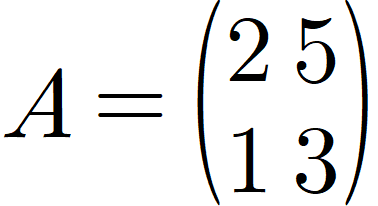
먼저, A의 역행렬을 구하면 아래와 같습니다.

 

이를 양변의 왼쪽에 곱해 줍니다.(행렬은 교환법칙이 성립하지 않습니다. 왼쪽에 곱해야 함을 잊지 마세요)

 

A와 A의 역함수는 단위행렬이 된어 좌변에는 a,b만 남습니다. 결국 우변만 계산하면 되네요

 

 

결국 a=1, b=1이였습니다.

역행렬은 이렇게 매우 큰 크기의 연립방정식도 쉽게 계산할 수 있는 방법입니다. 선형회귀식 역시 위 방법을 이용합니다.

② 선형회귀식 실제 구해보기

선형회귀식은 직선이 나온다고 생각해 보겠습니다.

우리가 구한 세 자료의 값이 각각 (-2, 0), (0, 2), (0,4)가 나왔다고 봅시다. 당연히 이 세 직선은 한 직선 위에 있지 않습니다.

그러므로 주어진 자료를 예측하는 완벽한 직선은 없습니다.

이때 우리는 이 세 자료의 경향성을 예측하려 합니다.

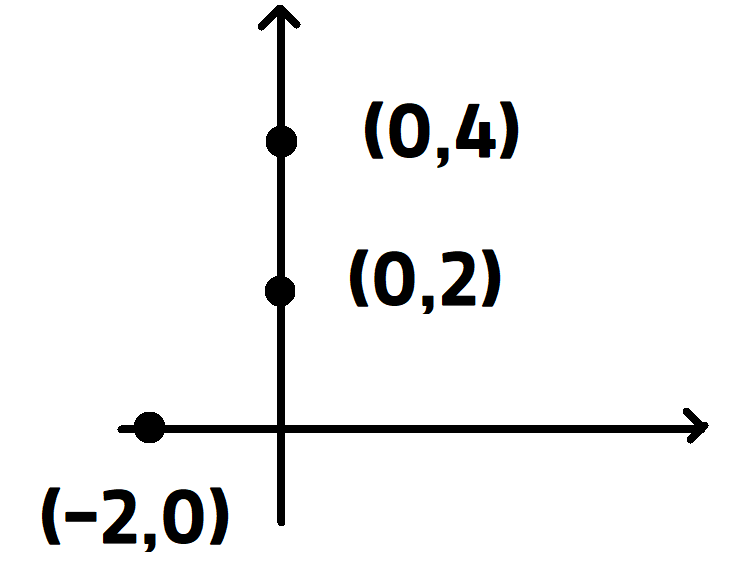
이제 저 세 자료(변수)의 경향을 알려 줄수 있는 직선 y=ax+b이 있다고 합니다.

이 직선에 주어진 세 변량을 대입하겠습니다.

 -2a+b = 0

0xa + b =2

0xa + b =4

가 나옵니다. 세 점을 모두 지나는 직선이 없으니 연립해서 a, b을 구할 수 없습니다.

위의 연립 방정식을 행렬로 표현 가능합니다.

 

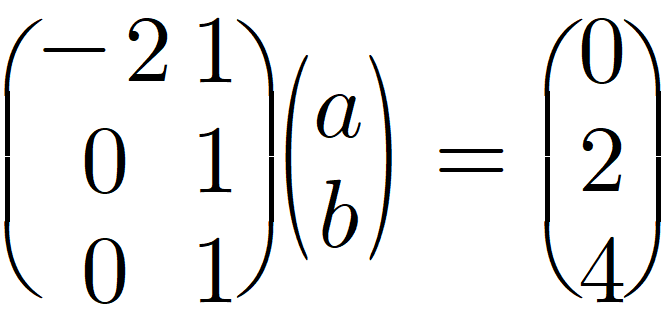
위의 좌변 행렬 곱셈을 계산하면 위에 a,b에 관한 방정식 세 개가 나옴을 확인할수 있을 것입니다.

특히, 좌변에 있는 3x2 행렬을 '계수행렬'이라고 부릅니다.

만약 계수 행렬의 역행렬을 구하면 ① 번의 방법으로 m, n을 구할 수 있을 것입니다.

만약 계수 행렬이 정사각 행렬이면 손쉽게 m,n을 구할 수 있습니다. ( numpy.linalg.inv 사용)

그러나 계수행렬이 정사각행렬이 아닙니다.

 

③ 유사역행렬(의사역행렬)

때문에 pinv, 즉, pseudo-inverse를 이용합니다.

유사역행렬은 정사각행렬이 아닌 A와 A의 전치 행렬을 이용해

m x n 행렬을 m, n 중 더 작은 값의 정사각행렬로 만듭니다.

 

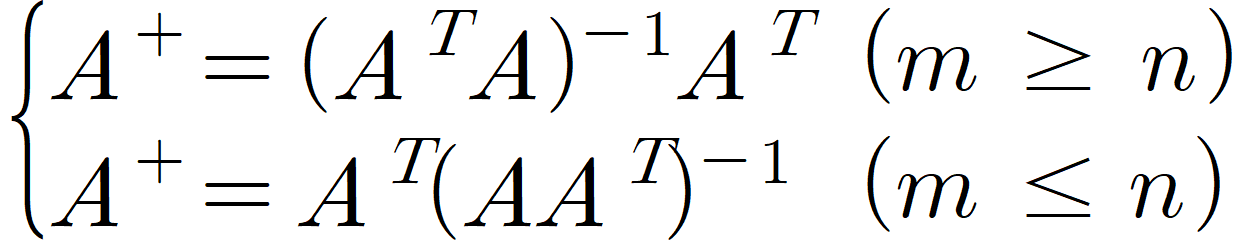
유사 역행렬은 위와 같이 사용되며 지수에 + 를 붙여 표현합니다.

또한 앞서 말한대로 곱셈의 교환법칙이 성립하지 않으므로 위와 같은 방향의 계산만 가능합니다.

이 부분도 유튜브에는 좀 더 자세히 설명했습니다.

이제 ②번에서 구한 계수행렬 A를 살펴보겠습니다.

3 x 2 이므로 m>n입니다. 그러므로 A의 유사역행렬을 구하면

 

 

 

이제 A의 유사역행렬을 이용하여 계수행렬로 표현된 행렬방정식을 풀어 보면

 

 

즉 a = 3/2 , b = 3이고 주어진 세 변량의 경량을 보여주는 회귀 직선은

 

 

 

이 나온다. 해당 직선의 그래프로 표현하면,  아래 그래프의 파랑 직선이 나온다.

 

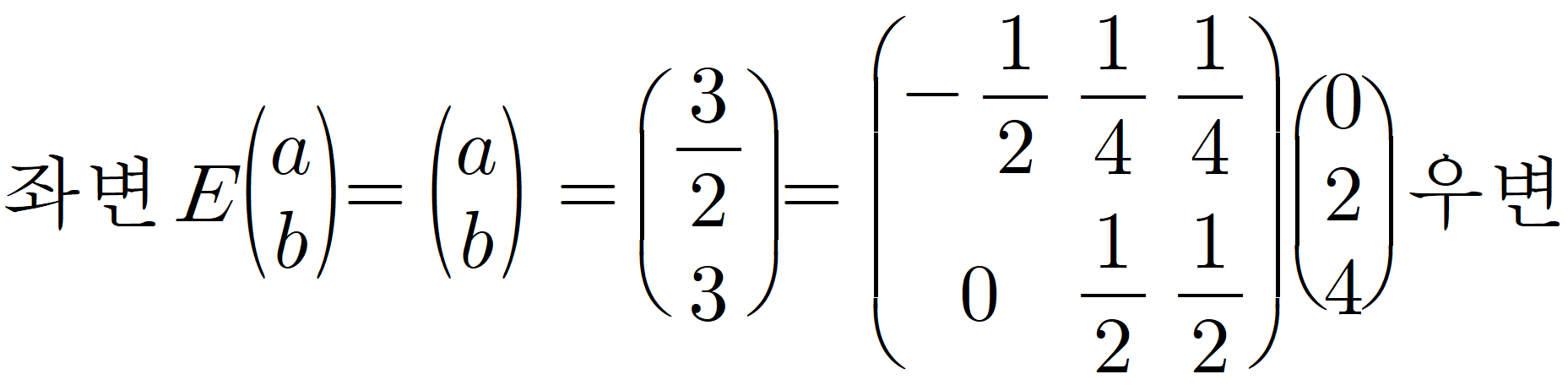
이렇게 numpy의 pinv 의 수학적 원리를 알아 보았다.

2변량 변수로 예제를 들어 이해를 도우려 했으나 실제 다변량 변수에서 더 큰 힘을 발휘하는 만큼 

선형회귀를 사용하는 것에 수학적 원리를 꼭 기억하길 바란다.

 

https://www.youtube.com/watch?v=vpGGwR1gUQA