선형회귀법의 수학적 원리(1) (기초행렬편)

[주요단어]

인공지능, 선형회귀, 파이썬, numpy, linalg pinv inv 행렬 수학 활용 벡터 직선의 방정식 연립 역행렬 가짜 유사 의사 무어-펜로즈 유사역행렬(Moore-Penrose) 컴퓨터 프로그래밍, AI, 경향성 예측

 

해당 내용은 가장 아래 유튜브 링크되어 있습니다. 읽는게 귀찮으신 분은

가장 아래쪽으로 내려가시면 유튜브 링크해 놓겠습니다.

 

1부 선형 회귀 이해를 위한 기초 수학

:이 부분을 자세히 알고 싶으신 분은 재생목록에 고급수학 행렬 강의 1~6강을 들으시면 됩니다.

 

① 행렬의 정의

:수나 문자를 직사각형의 형태로 배열하여 괄호로 묶어 나타낸 것

2X3 행렬

가로를 행이라고 부르고 세로를 열이라고 말함

위의 행렬은 2행 3열의 행렬

 

2X3 크기의 행렬 이라고 말한다.

 

보통 행렬은 대문자 알파벳을 써서 나타낸다. 

 

② 정사각행렬

m X m 으로 표현이 되는 행의 수와 열의 수가 같은 행렬을 정사각 행렬이라고 말한다.

흔히 m차 정사각행렬이라고 부른다.

2차 정사각 행렬

 

 

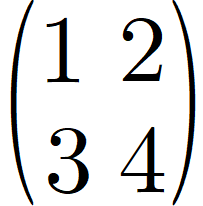
③ 대각성분

대각성분 이란 행과 열의 수가 같은 것을 이야기 한다. 1행 1열의 성분, 2행2열의 성분, 3행 2열의 성분

위의 행렬 B에서는 1, 5, 9가 대각성분이다.

 

⓸ 대각행렬

대각성분을 제외한 모든 성분이 0인 정사각행렬을 대각행렬이라고 부른다.

대각행렬

 

 

⓹ 단위행렬 E

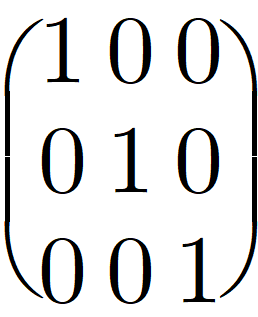
:단위행렬은 대각성분이 모두 1인 대각행렬을 의미한다. 행렬을 표현할 때는 대문자 E 또는 I 로 많이 사용한다.

 단위행렬의 경우는 행렬 곱셈 연산에서 수의 곱셈 1의 역할을 하는 중요한 행렬이다. 정사각행렬에서 정의된다.

3차 정사각행렬의 단위 행렬

 

⓺ 전치행렬

  m X n 행렬 A의 전치행렬은 A의 행과 열을 바꿔서 얻어진 n X m 행렬이다. 표현은 행렬 지수 부분에 대분자 T를 붙인다.

 

행렬 A의 전치행렬 A의 T제곱 표현

 

⓻ 행렬의 곱셈

 

 행렬의 곱셈은 A x B 일 때, 앞의 행렬의 열의 개수와 뒤에 곱하는 행의 수가 같아야지만 곱셈이 가능하다.

즉, 행렬A의 크기가 m x n 이고, 행렬B를 곱하고자 하는 경우 행렬 B의 행은 반드시 n이어야 한다.

그리고 행렬 B의 크기가 n x r이라면, 곱셈의 결과는 n을 제외한 m x r로 나온다.

 

위의 경우는 2x3 과  3x2를 곱하는 경우니 곱셈이 가능하고, 그 결과는 2x2로 나온다.

 

행렬 곱셈이 처음이라면 반드시 영상으로 설명을 듣기를 권한다.

글로만 확인할 경우 직관적으로 와 닿지 않는 내용이 존재할 수 있다.

 

앞의 행렬의 행과 뒤에 행렬의 열의 성분을 각각 순서대로 곱한 뒤 더한다. A의 1행과 B의 1열의 성분을 곱했다면,

그 결과를 1행 1열에 적어준다. 위의 작업을 반복하면 아래와 같다.

 

 

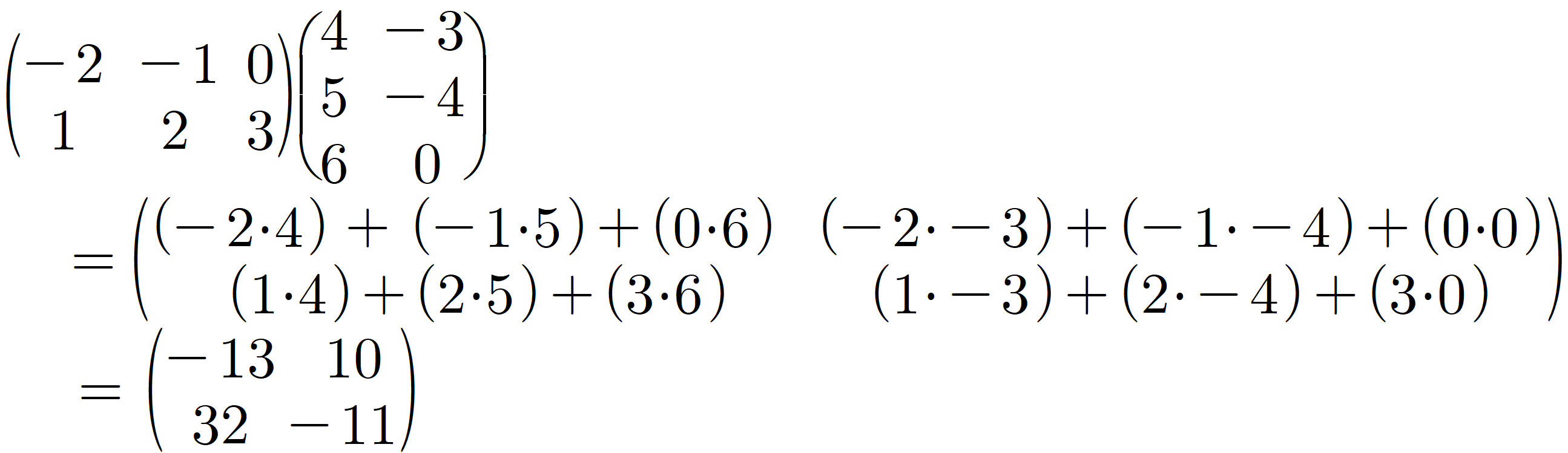
또한 행렬의 곱셈은 교환법칙이 성립하지 않는다. 위의 두 행렬을 계산해 보지 않더라도 

AxB는 2차 정사각행렬이 나왔지만, BxA는 3차 정사각행렬이 나옴을 알 수 있다.

 

⓼ 역행렬

역행렬은 정사각행렬 A가 있을 때, A x B = E, B x A = E를 만족하는 정사각행렬 B를 말한다.

먼저 행렬 곱셈을 배운 뒤이니 A x E = A, E x A = A가 되어 단위행렬E가 행렬 곱셈에서

숫자 곱셈 1의 역할을 함을 확인하자.

가우스소거법을 생략하고 우리의 목표인 선형회귀의 원리 설명을 위해

일반적인 2차 정사각행렬의 역행렬 공식을 소개한다.

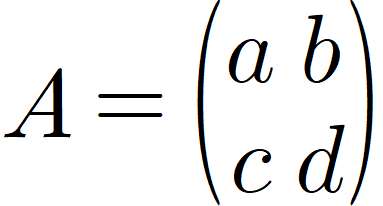
위와 같은 행렬 A에 대하여 A의 역행렬은 아래와 같음이 알려져 있다.

 

또한 역행렬의 표현은 A 인버스라고 하며 A의 지수자리에 -1을 적는다.

 

예를 들어 아래 행렬 B를 보자.

 

 

B의 역행렬은

 

이렇게 구할 수 있다. 실제로 B와 B의 역행렬을 실제로 곱셈 계산하면 단위행렬이 나옴을 확인할 수 있다.

 

https://www.youtube.com/watch?v=_eUd0Nasaa0