행렬의 기본 개념

행렬

: 행렬은 수나 문자를 직사각형의 형태로 배열하여 괄호로 묶어 나타낸 것

 

 

행렬에서 가로로 배열한 줄을 ‘행’ , 세로로 배열한 줄을 ‘열’ 이라고 합니다.

 

(2 –3 0.4 2/3)   1행

(3 4 1/2 –6)     2행

(-7 8 0 0)        3행

 

이라고 말할 수 있습니다.

 

그리고

 

 

이라고 말할 수 있습니다.

 

그리고 위와 같이 행이 3개 열이 4개 있는 행렬을 '크기'가 3 × 4인 행렬이라고 합니다.

그리고 행렬 안에 있는 각 숫자 하나하나를 행렬의 ‘성분’이라고 이야기 합니다.

 

일반적으로 행렬을 문자로 표현 할 때는 대문자 알파벳을 사용합니다.

위와 같은 행렬 A에서 성분을 표현하기 위해서 행을 i로 열을 j로 해서 A의 I행, j열을 로 표현한다.

 

 

즉, 위에서 예시로 든 행렬 A에서는

 

 

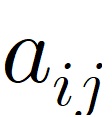
와 같이 표현 할 수 있다.

 

 

 

아래첨자를 ‘a_ij’로 표현하겠다.

블로그상의 같은 표현으로 이해해 주길 바란다

 

또한 i,j를 이용한 방법으로 행렬을 정의 할 수도 있다. 이렇게 정의하는 방법은 아래쪽에 문제로 다뤄 보겠다.

 

행렬 A의 ‘대각성분’은 a_11, a_22, a_33 ... 이고

행과 열의 숫자가 같으면 ‘정사각행렬’이라고 부른다. i × j 일 때, i=j이면 정사각 행렬이다.

 

그리고 대각성분을 제외한 모든 성분이 0인 행렬을 ‘대각행렬’이라하고, 특별히 대각성분이 모두 1인 대각행렬을 ‘단위행렬’이라고 한다.

 

 

 

A, B 모두 대각행렬이며 특히 B는 2 × 2 단위행렬이다.

 

서로 크기가 같고 대응되는 성분이 모두 같은 행렬은 ‘같다.’라고 쓰고 A=B로 표현한다.

 

문제를 통해서 배운 내용을 확인해 보겠습니다.

 

<문제1>

2 × 2 행렬 B의 (i, j)성분 b_ij 가 b_ij=i+j+1 이라 할 때,

에 대하여 A=B가 성립하도록 하는 x, y의 값은?

 

 

<해설>

b_11 = 1+1+1 =3

b_12 = 1+2+1 = 4

 

x=3이고

 

b_21 = 2+1+1 = 4

b_22 = 2+2+1 = 5

 

y=4

 

이다.

 

 

<전치행렬>

 

m × n 행렬 A의 ‘전치행렬’은 A의 행과 열을 바꿔서 얻어진 n × m 행렬이다.

 

 

즉 전치 행렬은 a_ij가 전치행렬의 a_ji가 된다고 생각하면 된다.

 

그리고 정사각행렬 중

인 경우를 대칭행렬이라한다.