점근선의 확장(지배항과 끝 변화 모델)
고등학교 수학으로 미적분 공부하기 시리즈 입니다.
글 마지막에 직접 제작한 동영상 링크해 두었습니다.
미적분학 학습을 위해서 만들었습니다.
고등학교 수학 내용을 바탕으로 심화, 확장해서 학습할 수 있도록 준비 했습니다.
해당 내용은 우리가 기존에 보지 못했던 형태의 그래프를 예측하고 대략적으로 그려 볼 수 있도록 도와주는 내용입니다.
<필요하신 분>
① 고등학교 수학, 수학I, 수학1 내용의 심화, 확장을 위한 공부를 하시는 분
② 그래프의 개략적인 변화, 공학적인 확인, 활용이 빠르게 필요하신 분
위와 같은 목적으로 공부하는 내용입니다.
오랜만에 영상으로 가볍게 시작하겠습니다.
<강의 순서>
① 점근선
② 지배항
③ 끝변화 모델
의 순서로 영상을 설명하도록 하겠습니다.
① 점근선
먼저 점근선을 확인해 보도록 하겠습니다.
고등학교 수학에서 가장 먼저 점근선을 배우는 때는 유리함수와 로그함수, 지수함수에 배울 것입니다.
간단히 확인해 보겠습니다.

주어진 식에서 점근선은 x=2, y=3입니다.
보통 그래프가 점근선에 한 없이 가까이 간다고 말합니다.
삼각함수를 배우신 분이라면 y=tanx의 그래프를 보면서 점근서이 여러 개가 될 수 있다는 사실은 이미 알고 있을 것입니다.
고등학교에서는 지수함수, 로그함수에서 추가로 점근선에 대한 내용이 있습니다.
그럼 이제 점근선을 이용해서 지배항 개념을 알고 파악해 보도록 하겠습니다.
② 지배항
수식을 하나 보면서 확인해 보겠습니다.

이라는 수식이 있습니다.
사실 우리는 미적분학을 배우면서 우리가 배운 모든 함수의 그래프를 그릴 수 있습니다.
하지만 아래 식을 보면 미분을 하고 싶은 마음이 많이 사라길 것입니다.
더불어 요즘은 그래프 그리는 프로그램이 너무 좋습니다.
지배항이라는 말은 간단하게 수직에서 실제의 값을 표현하는데 지배적인 역할을 하는 항이 있다는 것을 말합니다.
하지만 그래프 그리는 프로그램 없이도 간단하나 계산으로 그래프의 개형을 그릴 수 있습니다.
먼저 적당히 모양을 바꾸고 다항식의 나눗셈을 실시해 보겠습니다.

이렇게 식이 정리 됩니다.
이렇게 정리 된식을
y=(x/2)+1과 y=1/(2x-4)라는 두 개의 식으로 나누어 봅니다.
두 개의 그래프 모두 우리가 아주 쉽게 그릴 수 있는 그래프입니다.

그렇다면 이 그래프를 보면서 이야기 해 보도록 하겠습니다.
예를 들어 x=2 주변에서 살펴 보겠습니다.
x=2주변에서는 y=1/(2x-4)의 값이 무한대 혹은 마이너스 무한대의 값으로 변화합니다. 이 때, y=(x/2)+1의 값인 2라는 값이 전체 함숫값에 영향을 줄 수 있을까요?
아닙니다. x=2주변에서는 명백하게 유리함수 값이 전체 함수의 값을 결정하는데 결정적인 역할을 하고 일차함수는 그 값이 큰 역할을 할 수 없을 것입니다.
결국 전체 함수의 그래프는 x=2 주변에서는 유리함수 y=1/(2x-4)이 전체 함수를 지배하고 유리함수의 그래프와 비슷하게 그려질 것입니다.
즉, x=2주변에서는 유리함수가 지배항이 되는 것입니다.
마찬가지로 x의 값이 무한대로 커지거나 작아지는 상황을 보겠습니다.
이때는 유리함수 y=1/(2x-4)의 값이 점근선 y=0 에 한없이 가까워지고 전체 함숫값을 비교해 보았을 때, 0에 한 없이 가까운 값은 큰 영향을 줄 수 없고 다항함수 y=(x/2)+1의 값이 전체함숫값을 결정하는데 지배적인 역할을 할 것입니다.
실제 그래프도 다항함수와 유사하게 그려질 것입니다.
이렇게 지배항이라는 말은 실제 함숫값을 결정하는데 지배적인 역할을 한다는 말이고 이를 이용해서 함수의 그래프를 대략적으로 빠르게 그릴 수 있습니다.

③ 끝변화 모델
여기서 부터는 극한 개념을 배우신 분들만 보시면 됩니다.
끝변화 모델은 극한을 이용해서 위에서 배운 지배항의 개념을 확인하는 과정입니다.
먼저 가장 쉬운 다항함수로 예를 들어서 설명하겠습니다.

의 양 끝부분을 비교해 보겠습니다.
비교하는 방법은 간단합니다.
극한을 이용해서 비교하면
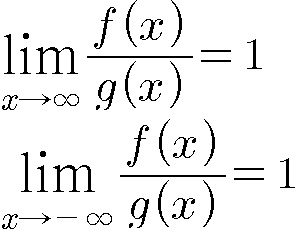
계산은 극한을 배운 사람들에게 는 너무 쉬운 내용입니다.
무한대와 마이너스 무한대에서 모두 1의 값이 나옵니다.
간단하게 생각해보면 f, g는 무한대나 마이너스 무한대의 값에서 비교해 보면 서로 같다는 말입니다.
즉 최고차항이 다항함수 전체를 지배한다는 말입니다.
끝변화 모델은 위에처럼 끝부분에서 지배하는 항을 말합니다.
여기서는 최고차항 3x의 네제곱이 좌, 우측 끝변화 모델입니다.

조금 어려운 예제를 하나 들겠습니다.
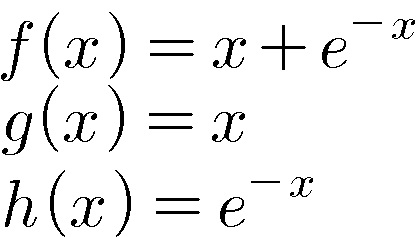
에서

즉, 함수 f의 우측 끝변화 모델은 g이고 h는 좌측 끝변화 모델이 될 것입니다.
그래프는 아래와 같습니다.

이렇게 지배항과 끝변화 모델만 확인하면 그래프를 대략적으로 파악할 수 있습니다.
특히 끝변화 모델을 잘 파악하면
특정 값 이상에서는 원래의 함수보다는 끝변화 모델만 사용해도 괜찮다는 사실을 알게 되면 공학과 컴퓨터 연산의 속도를 높이는데 큰 도움이 될 것이라고 생각합니다.
고등학생들에게는 고등학교 수학, 수학I, 수학1을 심화, 확장하는 공부를 하는 용도
고등학교 수준에서 보고서 작성하는 용도,
순수수학하시는 분들에게는 그래프의 개형 파악에도 도움이 될 것입니다.
오늘은 여기서 마치겠습니다.
https://www.youtube.com/watch?v=8O_TmaYx_yA